Minimal Planetary System with PyGame and Numpy
A few days ago I decided to look up the formula for planetary systems. As I read through the Wikipedia page about the n-body problem, I thought: It’s not too hard to implement. So I started with some random PyGame example and added the calculation for 2D planet movement.
In this post I will talk about some implementation details.
tl;dr the source code can be found here.

First things first, I created the Planet data structure:
Planet = recordtype('Planet', 'c v m')It stores the current coordinates, the velocity and the mass of a planet. The other important part is the drawing of the planets. I wanted a nice antialiased circle, so I used gfxdraw aa-functions for drawing. Here’s the whole drawing function:
def draw(p, surface):
x = int(p.c[0])
y = int(p.c[1])
if -100 < x < SCREEN_X + 100 and -100 < y < SCREEN_Y + 100:
pygame.gfxdraw.aacircle(screen, x, y, p.m, (255, 0, 0))
pygame.gfxdraw.filled_circle(screen, x, y, p.m, (255, 0, 0))It does not draw planets which are way outside the screen. Furthermore, the mass is just used for the radius which is just a shortcut. Feel free to add a real mass/area calculation.
Next up, the number crunching. Just as a reminder, here’s the formula (from Wikipedia):
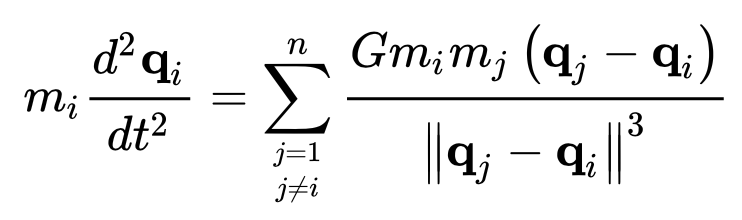
As you can see, we can take out the m_i. The formula describes the change of the velocity of an object (the acceleration) over time. This equals the sum of all forces by the other planets. G is just the gravitational constant and m_j is the mass of the other planet. The q’s are positional vectors, or in other words, a planet’s X- and Y-coordinate in this case. The ||q_j - q_i|| is in this case the distance between the planets (simple pythagorean theorem in 2D).
With this in mind, I created the following function which is called for each movement step:
def update_planets():
planets_copy = copy.deepcopy(planets)
for p, Q_i in zip(planets, planets_copy):
q_i = Q_i.c
d2q_i = 0
for Q_j in planets_copy:
if Q_j is not Q_i:
q_j = Q_j.c
d2q_i += G * Q_j.m * (q_j - q_i) / (np.hypot(q_j, q_i) ** 3)
p.v = Q_i.v + d2q_i
p.c = Q_i.c + p.vFirst I created a copy of the planets. Otherwise, we couldn’t change them inside the loop. Then we loop through both the planets and their copy at the same time by using zip(). d2q_i will be to sum which will be added to the velocity of the planet. The code calculates it by basically implementing the above formula. Please keep in mind, that the operations are vector operations and multiple (two) values are calculated at once.
Then we just need to update the current planet. This is done by adding d2q_i to the velocity of the planet and adding the planet’s velocity to the coordinates. Again, these are vector operations. That’s basically it for the movement calculations.
To make it a nice project, I added panning to be able to move the planets with the mouse. Furthermore, I wanted to make sure that the planets are not drifting away. My very cheap solution was to add an additional planet with a velocity (times mass) that is the opposite of the sum of all other planet’s velocity (times their masses).
The nice thing about using NumPy and implementing the formula with vectors is that is already generalized for n-dimensions. Here we used it for 2D, I may update the drawing part for some cheap orthogonal 3D (size of the planet is linear to the Z-coordinate?).
That’s it. The project was just a small one to see how fast and with how little code it is possible to implement such a planetary system.